Um problema geométrico envolvendo derivada

Eis aqui um problema que achei bem bonitinho e que envolve um conhecimento bem básico de Cálculo. Teoricamente, qualquer aluno que já aprendeu o que é uma derivada (em especial a interpretação geométrica) está apto a fazê-lo. Segue o problema e sua resolução:

Mostre que a área do triângulo formado pelos eixos x, y e a reta tangente ao gráfico de , em qualquer ponto, é igual a 2.

Resolução

Antes de mais nada, precisamos entender o problema. Vamos plotar o gráfico de.


Feito isto, precisamos tomar um ponto qualquer no nosso gráfico e traçar uma reta tangente à função neste ponto. Visualmente, é fácil ver como esta reta tem que ser, mas vamos precisar da equação desta reta.


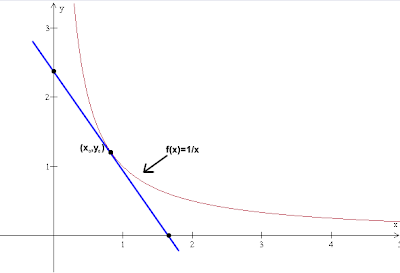
A equação geral de uma reta qualquer é dada por , onde é um ponto conhecido da reta e m é o coeficiente angular.

O ponto da reta já temos, aliás, é o próprio genérico que vamos usar. Agora, valendo 1 milhão de reais, como vamos achar o coeficiente angular? Que rufem os tambores!

Eu ouvi dizer derivada? Sim! Afinal, uma das possíveis interpretações da derivada de uma função num ponto (conhecida como interpretação geométrica), é a que diz que a derivada é o coeficiente angular da reta tangente à função naquele ponto.

Sabendo disso, basta então derivar a nossa função e calculá-la no ponto assim vamos obter o m, isto é, o coeficiente angular da reta que queremos.

A derivada de é . No ponto , teremos . Portanto, nossa equação da reta (azul) ficará assim:



Das aulas de matemática da escola, sabemos que a área de um triângulo é dada por onde b é a base e h é a altura. No nosso caso, como o triângulo é retângulo a base será o valor da intersecção da reta azul com o eixo x e a altura será a intersecção da reta azul com o eixo y.

Portanto, só nos falta calcular estas intersecções. No eixo x, temos:



Então . Como , temos

. Resolvendo em x, obtemos .

Por simetria, podemos inferir que . Caso não esteja convencido disso, basta calcular a intersecção da reta azul com o a reta x=0, parecido como fizemos no caso anterior.

Pronto, nossa base é e nossa altura é . Aplicando na fórmula da área () do triângulo teremos:



Mas lembre-se que , portanto

. Como queríamos demonstrar.

Até.