Problemas LeGauss: Problema A1 - Putnam 2009

O seguinte problema foi proposto na Putnam em 2009:

Seja uma função tal que para todo quadrado no plano, tem-se . É verdade que para todo ponto do plano?

Minha solução difere um pouco da solução oficial que pode ser encontrada aqui. Vamos à ela:

Sim, é verdade. Considere um ponto qualquer no plano. Agora, posso escolher um outro ponto (que se situa na pontinha do vetor desenhado) de forma que o vetor que liga ele à faz 45º com o eixo horizontal e o eixo vertical que passam por .



Realizando reflexões nestes vetores, posso formar o quadrado , como na imagem que segue:



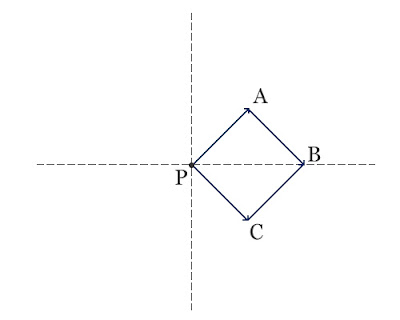
De forma completamente análoga, posso formar também os quadrados , e (a partir de agora vou omitir as setinhas dos vetores para não carregar a figura).



Pela hipótese do problema, segue que

Somando todas as equações e reordenando os termos, temos

Note que e são quadrados (o primeiro está em verde e o segundo em vermelho).



Logo,

Até.