Vamos experimentar somas diferentes?

Durante a graduação, aprendemos (e bem) a integrar funções reais e, dependendo do curso, complexas (a uma variável, ao menos). E em geral nos baseamos na integral dada pela definição de Riemann. Vamos rapidamente definir esta integral, de forma coloquial e descontraída, para mais adiante mostrar uma outra definição para esta a integral. Esta nova definição nos traz diversas facilidades (e dificuldades), mas faz parte de um estudo importantíssimo para a física e para a matemática (é a base para a teoria da probabilidade, estatística, teoria ergódica, etc).

Integral usual

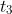O intervalo entre dois números reais e é denotado por . Se for uma função real nesse intervalo, então podemos particionar o intervalo , sendo os pontos que iniciam e finalizam cada partição os . A cada intervalo, indicamos um ponto interior (ao intervalo), denotado por . Por exemplo, no intervalo temos o número . A soma de Riemann então desta função é dada por

Gostaríamos que esse valor, , fosse a área sob a curva definida por no intervalo. O mais fabuloso dessa história toda é que a grandeza de fato converge para essa área quando as diferenças tendem a zero para uma grande gama de funções. O número de partições, naturalmente, cresce de forma exorbitante. Quando tomamos esse processo limite, transformamos a soma de Riemann na intergral de Rieman.

Teoria da Medida

Sabe aquelas pessoas que sempre que ouvem um assunto sobre o qual já leram alguma pegadinha ou detalhezinho, acabam provocando alguma discussão nesse sentido? Pois é, por meio de pessoas assim e livros afins, existe um exemplo interessante que ficou famosíssimo. Suponha que, por algum motivo, desejamos integrar a função

É possível? A pergunta mais natural, até mais que esta primeira: a resposta é intuitiva? A mim, não parece nada intuitiva. E é neste contexto [1] que surgiram métodos mais elegantes para o cálculo de integrais. A Teoria da Medida, uma extensa área autosuficiente [2] da matemática que tenta extender a noção de "área" (comprimentos, áreas, volumes, etc), entra como sendo o centro da definição mais utilizada de integração: a integral de Lebesgue-Stieltjes. Mas não se assuste: sinteticamente, apenas o nome ficou mais feio. Como agora temos mais de uma definição (ou técnicas) de integração, cria-se a chamada Teoria de Integração, o que vamos tratar aqui apenas como o estudo destas técnicas.

Mas como toda teoria charmosa, a Teoria da Integração dá nomes interessantes. Freqüentemente, encontramos as integrais de Lebesgue, desacompanhadas de Stieltjes. Isto porque a integral de Lebesgue é a extensão da integral de Riemann usando medidas muito especiais: a medida de Lebesgue [3]. Trata-se do caso mais recorrente e o que vai tomar um pouco de nossa atenção. Para as demais medidas e a maioria dos casos, usamos o nome Stieltjes ou Radon acompanhando o de Lebesgue.

Medida de Lebesgue

A medida de Lebesgue pode ser compreendida como uma função que atribui a toda região de um espaço Euclidiano um valor real positivo (ou infinito, inclusive). Este valor é o que chamamos de comprimento, área ou volume, se a região tem dimensão 1, 2 ou 3 (respectivamente). O intervalo anterior, , teria, na reta real, que medida? Essa é uma pergunta que não deve ser feita: nós é que definimos a medida. Mas pensando na medida usual, aquela em que o resultado teria que coinscidir com o resultado usado por uma régua, poderíamos definir como sendo a diferença . Então, podemos definir a função como [4]

Faz sentido perguntarmos de conjuntos em que ? Para que isto ocorra, . Estes são os conhecidos conjuntos de medida nula. Mesmo se não definirmos dessa forma óbvia, ainda assim poderíamos ter conjuntos de medida nula.

Integral de Lebesgue

Mas e quanto à integral? Lembra-se da definição da soma de Riemann dada logo acima? Então, podemos reescrevê-la usando uma medida qualquer, definindo com isto a soma de Lebesgue

A definição dos termos são os valores da função escolhidos de forma esperta (utilizamos funções simples). Ao tomarmos um processo limite parecido com aquele em que fazíamos a as partições terem comprimentos cada vez menores para a soma de Riemann, a soma de Lebesgue transforma-se na integral de Lebesgue. Obviamente, para diferentes medidas, a integral deve mudar. Mas se usarmos aquela medida mais óbvia, aquela usual que definimos logo antes nos baseando na reta real, então a integral de Lebesgue deve coincidir exatamente com a integral de Riemann. A diferença está no seguinte...

Toda função Riemann integrável é Lebesgue integrável, mas nem toda função Lebesgue integrável é Riemann integrável.

Assim, há funções que poderemos integrar utilizando a definição de Riemann e há funções que só poderíamos integrar usando a definição de Lebesgue (ou Stieltjes, Radon, etc). Portanto, se pudermos calcular a integral via Lebesgue, já será o suficiente.

A definição da integral de Lebesgue sugere uma soma, assim como a de Riemann, só que com um peso diferente: o peso é a medida do intervalo. Imagine duas funções quaisquer. Suponha que em todo o domínio estas funções sejam idênticas, a menos de um único conjunto de valores. O que deve ocorrer se esse conjunto de valores tiver medida nula?... Isso mesmo, a integral de ambas deverá ser igual [5]. Unindo estas últimas informações à citação acima, podemos sempre calcular via Lebesgue as integrais apenas tomando cuidado com os conjuntos de medida não nula. Motivo, aliás, pelo qual a integral da função é nula.

Aplicação direta.

Eu costumo me sentir muito mal quando falo, falo, falo, e não apresento nenhum exemplo. Vamos tentar integrar uma função, que não aquela que mensionei acima (nula se argumento é irracional, senão 1). Eu gostaria de integrar a função [6]

Não se assuste com o nome: é um conjunto conhecido como reais estendidos e serve para adicionarmos à brincadeira o [7]. Portanto, pode assumir qualquer valor, inclusive infinito. A primeira coisa que podemos ver é que assume valor não nulo (e, portanto, contribui para a integral) apenas no conjunto , que refere-se ao intervalo [0,0]. Como naturalmente gostaríamos de conhecer sua integral via medida de Lebesgue com medida usual, sabemos qu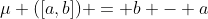e e . Portanto, é nula a menos de um conjunto de medida nula. Com base nisso, concluímos que

Esta é a aplicação mais simples e menos viciada que pude encontrar, além de podermos explorar uma função que freqüentemente encontramos em livros. Notemos, por fim, que é identicamente nula [5].

Notas:

1. Não tem nada a ver, historicamente, com a função maluca que nos propusemos a integrar.
2. Palavras do professor Hernandes, trata-se de uma teoria que se baseia no estudo de funções muito específicas e necessita apenas de Teoria de Conjuntos, mas que aplica-se a inúmeras áreas (probabilidades, integração, grupos, etc). Para uma idéia da aplicabilidade desta teoria, veja os Axiomas de Kolmogorov, que geram toda a probabilidade (e, naturalmente, formam um conjunto axiomático "isomórfico" às outras maneiras de se "compreender" a teoria da probabilidade.
3. Se alguém sugerir algum artigo bom para linkar, eu adicionarei aqui!
4. Sim, é uma função de um conjunto.
5. Se uma função tem integral nula a menos de um conjunto de medida nula, então chamamos esta função de identicamente nula.
6. Não, esta não é a Delta de Dirac, e portanto a resposta não precisa necessariamente ser 1.
7. Talvez assunto para outro post... Se esse funcionar ^^

Post Scriptum:

Gostaria de agradecer a discussões prévias com Brenno G. Barbosa, grande colega com quem me graduei mas que infelizmente mudou-se de instituto. Saudações a ele!

Este texto é uma republicação. Veja o original e os comentários do original aqui. Algumas alterações foram feitas para que o texto adeque-se melhor ao Legauss.

Atualizações:

1. Assim como sugerido em comentários, especifiquei alguns detalhes sobre a definição da integral de Lebesgue.