O plano projetivo, a combinatória e o tênis.

E aí galerinha do LeGauss!

Ultimamente tenho estudado geometria projetiva e tenho gostado muito do assunto, o livro que estou lendo é o Projective Geometry: From Foundations to Applications do Albrecht Beutelspacher e do Ute Rosenbaum.
Ele é muito bom, eu peguei ele inocentemente pra ler e acabei achando a leitura leve, descobri que o livro de onde eu tirei o problema que eu vou resolver nesse post colocava esse livro como referência bibliográfica em vários cápitulos. (Esse livro tem referências em cada capítulo, só para constar.)

Bom, o problema foi retirado do livro 21 Aulas de Matemática Olímpica do Shine, publicado pela SBM

O livro tem vários problemas legais e me ajudou bastante a ver como utilizar o plano projetivo em problemas de combinatória, eu recomendo, mas vou avisando que o livro é BEM rápido. (não tem nada muito didático nele xD).
O livro do Beutelspacher e do Rosenbaum, também tem várias aplicações em combinatória (aplicações em comunicação e criptografia), mas ele fala mais profundamente sobre geometria projetiva e eu ainda não cheguei nas partes de aplicações.

O problema é o seguinte:

"Um torneio de tênis é disputado entre duas equipes. Cada membro de uma equipe joga com um ou mais mebros da outra equipe, de modo que:
(i) dois membros de uma mesma equipe têm exatamente um oponente em comum;
(ii) não existem dois membros de uma equipe que enfrentam, juntos, todos os membros da outra equipe.
Prove que cada jogador deve jogar um mesmo número de partidas."

Primeiro pra resolvermos esse exercício vou falar rapidamente sobre o que é um plano projetivo.

Um plano projetivo é uma tripla (,,), onde chamamos de o conjunto de pontos, de conjunto de retas e a relação de incidência, que dita se um ponto pertence a uma reta.

Um plano projetivo obedece os seguintes axiomas:

1. Dados dois pontos sempre existe uma, e somente uma, reta incidente a eles;
2. Dadas duas retas quaisquer, elas sempre se cruzam em exatamente um ponto;
3. Existem pelo menos 4 pontos tais que, dentre eles 3 não estão contidos em uma mesma reta.

Com esses axiomas conseguimos também mostrar que:

(a) Existem pelo menos duas retas;
(b) Toda reta tem pelo menos 3 pontos.

(Na verdade o axioma 3 pode ser substituído pelas propriedades (a) e (b).)

Outra propriedade importante do plano projetivo é o:

Princípio da dualidade:

Se uma afirmação é válida no seu plano projetivo, se você trocar a palavra ponto por reta e reta por ponto essa nova afirmação também valerá (essa nova afirmação é também chamada de afirmação dual).

Exemplo: Sabemos que "Dados dois pontos, eles são incidentes a exatamente uma reta." (pelo axioma 1, logo a afirmação dual também vale: "Dadas duas retas, elas são incidentes a exatamente um ponto." Que é exatamente o que diz o axioma 2!

(Para demonstrar o princípio da dualidade, basta motrar que o dual de todos os axiomas do plano projetivo, também valem, você pode ver uma demonstração disso, por exemplo, no livro do Beutelspacher e do Rosenbaum.)

Bom, é isso o que eu tenho a dizer sobre o plano projetivo, se quiser mais informações leia o livro citado acima.

A dificuldade desse problema é na verdade ver que os nossos jogadores se comportam como um plano projetivo! Eu sei que parece estranho, mas é verdade!

Repare que podemos ver os jogadores de uma equipe como o conjunto de pontos de um plano projetivo, os jogadores da equipe adversária como as retas e dizer que uma reta é incidente a um ponto (e vice-versa) se os dois membros jogaram um com o outro!

Temos que mostrar que as condições do nosso problema realmente tornam essa "coisa" um plano projetivo.

Para facilitar, vou chamar a equipe que é representada pelos pontos de equipe e a equipe representada pelas retas de equipe .

O axioma 1. diz que dados dois pontos, deve existir uma, e somente uma reta, que passa por eles.
Isso é verdade por que dados dois jogadores da equipe eles têm exatamente um adversário em comum, isso é, existe exatamente uma reta que representa esse adversário em comum, que é incidente aos dois pontos que representam esses membros.

O axioma 2. diz que dadas duas retas, elas se cruzam em exatamente um ponto. Isso também é verdade por um raciocínio completamente análogo ao anterior. Duas retas sempre se cruzam em um ponto por que dados os jogadores e da equipe eles têm exatamente um adversário em comum, logo suas retas se cruzam no ponto que representa esse adversário.

O axioma 3. é fácil de enxergar e difícil de explicar sem usar a geometria (que eu não quero usar para não confundir).
Vamos pegar 2 pontos e . Eles têm um adversário em comum, isto é, existe uma reta que passa por eles.
Mas, está sozinha enfrentando o time adversário inteiro, o que contraria a segunda hipótese do enunciado do nosso problema, logo existe um terceiro ponto, , que não pertence à , perceba que disputou um jogo com alguém, e mais que isso, ele tem um adversário em comum com e outro com , o adversário em comum com eu chamarei de e com chamarei de

Agora note que qualquer par de membros da equipe está enfrentando a outra equipe inteira, o que também contraria nosso enunciado, então existe um ponto que não pertence a nenhuma dessas retas (caso pertencesse ainda existiria um par de retas que enfrenta a outra equipe inteira). E isso prova que o axioma 3 é satisfeito e nos mostra que temos um plano projetivo em mãos.

Se você não entendeu a parte do terceiro axioma, leia de novo e vá desenhando um diagrama com os pontos e as retas, provavelmente ajudará a ver o que eu estou dizendo.

Bem, o problema já está acabado, pois uma propriedade importante de um plano projetivo é que, qualquer reta possui o mesmo número de pontos, digamos (e qualquer ponto também possui o mesmo número de retas incidentes a ele, que também será , pelo princípio da dualidade).

Como isso é o problema em si eu vou demonstrar este resultado, mas isso vou fazer geometricamente, vou mostrar que essa propriedade vale para qualquer plano projetivo, logo valerá para o nosso caso.

Vamos pegar um plano projetivo . Ele possui duas retas, pela propriedade (a) e elas se cruzam em um ponto, pelo axioma 2, vamos chamar esse ponto de , além disso existe um outro ponto em cada uma dessas retas, pela propriedade (b), vamos chamá-los de e .



Vou chamar a reta de e a outra de .

Note que é uma nova reta, logo possui um terceiro ponto que não vai pertencer às anteriores (pela propriedade (b)!) que chamarei de



Agora, veja que consigo criar uma bijeção definindo 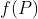como o ponto em que a reta corta a reta (Note que .)



E isso termina nossa demonstração e nosso exercício!
Espero que tenham curtido.
Até a próxima.