
Não é só em futebol que falamos em bolas quadradas, na matemática uma bola também pode ser quadrada. O interesse por esse post nos leva a um dos estudos mais interessantes da matemática: os espaços métricos. De forma simples, um espaço métrico nos remete à noção de uma coleção em que podemos dizer quão longe um objeto está de outro. Por exemplo, quando dizemos quão longe nossa mesa está das garrafas de cerveja. Mas como fazer isso? Definindo uma distância (no caso, a fita métrica).
Para definir um espaço métrico precisamos de duas coisas: um conjunto, que será a coleção de objetos, e uma função, definida nesse conjunto todo, cuja imagem indica a distância entre dois objetos. Algo assim: se é um conjunto, então definimos a função
é um conjunto, então definimos a função

Esta função é o que entenderemos como distância. Se , então a distância entre
, então a distância entre  e
e  é
é  . Para que esta função possa ser encarada como uma distância, é necessário que ela satisfaça alguns axiomas:
. Para que esta função possa ser encarada como uma distância, é necessário que ela satisfaça alguns axiomas:
Que tal mais algo mais experimental? Vamos tentar escrever a função distância para o conjunto de vetores de um espaço euclidiano? Então, suponha que seja um conjunto de vetores; vamos adicionar um produto escalar já definido:
seja um conjunto de vetores; vamos adicionar um produto escalar já definido:  . A partir do produto escalar, definimos a norma de um vetor:
. A partir do produto escalar, definimos a norma de um vetor:

Sendo assim, podemos definir a distância entre dois vetores e
e  como
como

uma vez que a subtração está definida. Como a norma é sempre real, a imagem de é não negativa para quaisquer dois vetores
é não negativa para quaisquer dois vetores  e
e  .
.
Diversas coisas que utilizamos em matemática dependem dessa noção, embora isso possa não ter ficado ainda muito claro. Por exemplo, qual a definição de uma circunferência? Vamos juntos:
 Ótimo. Como é a forma de uma bola então? Arredondada, sem lados, esféricamente simétrica. Esfericamente?... Note que a imagem que temos de uma bola depende intimamente da definição da distância: se modificássemos a função distância, mas continuassemos a procurar por um lugar geométrico formado pelos pontos equidistantes a um dado ponto, obteríamos o que?
Ótimo. Como é a forma de uma bola então? Arredondada, sem lados, esféricamente simétrica. Esfericamente?... Note que a imagem que temos de uma bola depende intimamente da definição da distância: se modificássemos a função distância, mas continuassemos a procurar por um lugar geométrico formado pelos pontos equidistantes a um dado ponto, obteríamos o que?
Mais uma vez, vamos experimentar! Vamos definir uma função distância bem problemática. Vamos trabalhar no plano, com . E para facilitar, colocamos o centro da circunferência na origem, ou seja, no ponto
. E para facilitar, colocamos o centro da circunferência na origem, ou seja, no ponto  . Para dois vetores
. Para dois vetores  e
e  , sugerimos a seguinte função:
, sugerimos a seguinte função:

Qual a primeira pergunta que somos obrigados a responder? Se ela satisfaz os axiomas dados acima. Talvez o mais complicado seja verificar a desigualdade triangular, mas vamos deixar isto de lado um pouco. Vamos ver então o que é uma circunferência se estivermos lidando com esta função distância?
Primeiramente, podemos formular este problema da seguinte forma: gostaríamos de obter todos os pares de reais que satisfazem a equação
de reais que satisfazem a equação

 em que
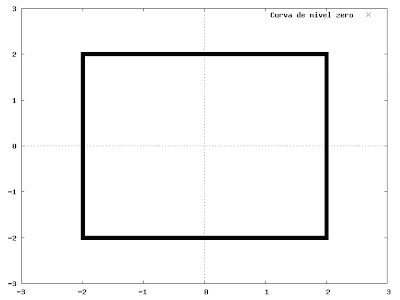
em que  é o raio dessa circunferência. E qual a solução para este problema aparentemente simples? Sim, a solução está graficada à direita (clique na figura para aumentá-la): uma bola quadrada! O gráfico mostra a solução para o caso em que o raio é 2.
é o raio dessa circunferência. E qual a solução para este problema aparentemente simples? Sim, a solução está graficada à direita (clique na figura para aumentá-la): uma bola quadrada! O gráfico mostra a solução para o caso em que o raio é 2.
Não é difícil prever que a solução seria assim, basta esquematizar as regiões independemente. Por exemplo, uma das coordenadas mantém-se igual ao raio enquanto a outra deve variar seu valor de a
a  . Esquematizando quais as possíveis combinações, chegamos à conclusão de que o lugar geométrico que obedece essas novas regras é um quadrado.
. Esquematizando quais as possíveis combinações, chegamos à conclusão de que o lugar geométrico que obedece essas novas regras é um quadrado.
O gráfico foi obtido com um script python. Sabe o que é mais legal? Testar novas funções e ver o resultado da brincadeira. Por isso, segue abaixo o script python já pronto pra gerar um gif com o resultado usando o gnuplot. O script também já fornece a superfície gerada pelas distâncias dos pontos, caso alguém possa querer utilizar.
Importante: o script está preparado para encarar sistemas com Windows e Linux, basta que o gnuplot esteja instalado.
Download
E o que fazemos com a bola quadrada?!

Se você achar qualquer coisa estranha, envie-nos um comentário!
Boa diversão!
Para definir um espaço métrico precisamos de duas coisas: um conjunto, que será a coleção de objetos, e uma função, definida nesse conjunto todo, cuja imagem indica a distância entre dois objetos. Algo assim: se
Esta função é o que entenderemos como distância. Se
sse
.
.
.
Que tal mais algo mais experimental? Vamos tentar escrever a função distância para o conjunto de vetores de um espaço euclidiano? Então, suponha que
Sendo assim, podemos definir a distância entre dois vetores
uma vez que a subtração está definida. Como a norma é sempre real, a imagem de
Diversas coisas que utilizamos em matemática dependem dessa noção, embora isso possa não ter ficado ainda muito claro. Por exemplo, qual a definição de uma circunferência? Vamos juntos:
Circunferência é o lugar geométrico de todos os pontos de um plano que equidistam de um mesmo ponto. A distância até o ponto é chamada de raio e o ponto é chamado de centro.
Mais uma vez, vamos experimentar! Vamos definir uma função distância bem problemática. Vamos trabalhar no plano, com
Qual a primeira pergunta que somos obrigados a responder? Se ela satisfaz os axiomas dados acima. Talvez o mais complicado seja verificar a desigualdade triangular, mas vamos deixar isto de lado um pouco. Vamos ver então o que é uma circunferência se estivermos lidando com esta função distância?
Primeiramente, podemos formular este problema da seguinte forma: gostaríamos de obter todos os pares
 em que
em que Não é difícil prever que a solução seria assim, basta esquematizar as regiões independemente. Por exemplo, uma das coordenadas mantém-se igual ao raio enquanto a outra deve variar seu valor de
O gráfico foi obtido com um script python. Sabe o que é mais legal? Testar novas funções e ver o resultado da brincadeira. Por isso, segue abaixo o script python já pronto pra gerar um gif com o resultado usando o gnuplot. O script também já fornece a superfície gerada pelas distâncias dos pontos, caso alguém possa querer utilizar.
Importante: o script está preparado para encarar sistemas com Windows e Linux, basta que o gnuplot esteja instalado.
Download
E o que fazemos com a bola quadrada?!

Se você achar qualquer coisa estranha, envie-nos um comentário!
Boa diversão!

13 comentários:
até a metade do post eu fiquei me perguntando se os t(h)iagos tinham trocado de papel...
... :(
Problema: script está sem identação. Acerto isso logo.
Agora só falta plotar o Kiko =} he he he
Muito legal o artigo, a gente já tinha discutido um pouco disso. Mas eu não o teria feito tão bem. ;-)
Eu achei dois erros que vc deve ter cometido pela pressa (ou quem sabe sou eu que estou errado).
Primeiro. Se a norma que você está utilizando é a euclidiana, quando você diz " A partir do produto escalar, definimos a norma de um vetor:"
A norma deveria estar ao quadrado ou o (a,a) deveria estar com uma raiz quadrada.
Segundo. Quando você diz " Sugerimos a seguinte função:" a função não seria:
d(x,y)=max(|x_1 - x_2|,|y_1 - y_2|)
?
Bem, me corrija se eu estiver errado.
Anyway, a matemática pode concretizar o sonho do Kiko!
Primeira pergunta. Sim, falta uma raiz : )
Segunda pergunta. x e y são vetores e usualmente denotamos as coordenadas dos vetores com índices.
Gostaríamos que fosse o máximo entre a coordenada x de cada um e y de cada outro. Certo? Tipo... a função leva dois vetores a um real, certo? Então x_1 - y_1 é a diferença entre a primeira coordenada. A função que você sugeriu é apenas diferente. Tanto que se tomarmos y como o vetor 0, então teremos que achar a curva de nível da superfície
max(|x_1-X_2|,0) - r = 0 ,
que fornece algo bem diferente.
Entendi, mas então você deveria deixar mais claro que x=(x_1,x_2) e y=(y_1,y_2). Eu, pessoalmente, não gosto dessa notação, me confunde.
Ou então, coloque d((x_1,x_2),(y_1,y_2)).
Mas eu bobeei, obviamente, a distância é entre dois vetores então fica implícito que x=(x_1,x_2) e y=(y_1,y_2). Mas coisas implícitas podem passar desapercebidas. =P
Feito. Veja se está 'sutil' demais ainda e me avise.
Agora tá bom. ;-)
Interessante...
Ainda não sei a origem do termo "bola", mas o interessante é como o conceito de bola é generalizado quando estudamos espaços topoloógicos ...
"Bola" ou abertos podem ser coisas estremamente estranhas .. e complicadas ..
... em espaços métricos, o termo bola já recebe outro significado. O bola do texto é o primeiro sentido do dicionário.
Boa Yoko!! Quando a gente vai abstrair mais começar a falar de topologia?? Haha!!
Postar um comentário