Olá galerinha do LeGauss.
Vou provar hoje um teorema útil para calcular sólidos de rotação.
O teorema do centróide de Pappus diz que o volume gerado pela rotação de uma figura ao redor de um eixo (no mesmo plano que ela e que não a intercepta) é dado por:
Onde
é a distância do centróide da figura (o centro de massa) até o eixo de rotação e 
é a área da figura.
Vou provar hoje um teorema útil para calcular sólidos de rotação.
O teorema do centróide de Pappus diz que o volume gerado pela rotação de uma figura ao redor de um eixo (no mesmo plano que ela e que não a intercepta) é dado por:
Onde
é a distância do centróide da figura (o centro de massa) até o eixo de rotação e é a área da figura.O centróide é dado pelas seguintes equações no caso 2-dimensional:
Agora vamos a prova:
Inicialmente temos a seguinte situação:
Vamos escolher de forma "malandra" que nosso segundo eixo passe pelo centro de massa. Repare que isso não resulta em nenhuma perda de generalidade:
Agora, dividimos nossa figura em vários retangulozinhos de base
e altura 
.
Note que o volume do nosso sólido de rotação vai ser a soma de todos os anéis que esses retângulos gerarão ao darem a volta no eixo.
Vamos chamar de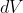
o volume desses anéis, logo temos:
Eu joguei fora no meio dessas contas um termo do tipo
, vendo isso da forma Leibniz de lidar com as coisas, esse cara é um infinitesimal de ordem superior e a integral dele continua sendo um infinitesimal. haha
Mas isso é facilmente formalizado usando séries infinitas, se quiser faça as contas aí. Além disso eu chamei
, caso alguém não tenha entendido.
Repare o que achamos então:
Que é exatamente a fórmula que desejávamos.
Espero que tenham curtido até. ;^)
Link:
Se você gostou do teorema veja também o que o blog Fatos Matemáticos tem a dizer sobre ele =P
Fatos Matemáticos - O Elegante Teorema de Pappus
Agora vamos a prova:
Inicialmente temos a seguinte situação:
Vamos escolher de forma "malandra" que nosso segundo eixo passe pelo centro de massa. Repare que isso não resulta em nenhuma perda de generalidade:
Agora, dividimos nossa figura em vários retangulozinhos de base
e altura .Note que o volume do nosso sólido de rotação vai ser a soma de todos os anéis que esses retângulos gerarão ao darem a volta no eixo.
Vamos chamar de
o volume desses anéis, logo temos:Eu joguei fora no meio dessas contas um termo do tipo
, vendo isso da forma Leibniz de lidar com as coisas, esse cara é um infinitesimal de ordem superior e a integral dele continua sendo um infinitesimal. hahaMas isso é facilmente formalizado usando séries infinitas, se quiser faça as contas aí. Além disso eu chamei
, caso alguém não tenha entendido.Repare o que achamos então:
Que é exatamente a fórmula que desejávamos.
Link:
Se você gostou do teorema veja também o que o blog Fatos Matemáticos tem a dizer sobre ele =P
Fatos Matemáticos - O Elegante Teorema de Pappus
7 comentários:
Bem interessante, publiquei algo semelhante no Fatos Matemáticos.
Adicionei um link para o seu post, obrigado por comentar.
Além de intuitivo, a demonstração deste teorema é bem simples, mas não lembro de ter visto em cálculo. =/
Tiago e adms, perdão pelo off-topic, mas tentei entrar em contato com vocês pelo email sugerido no rodapé, e parece que, segundo o gmail, o endereço não existe. Eu tentei...
letterstoeditoreslegauss@gmail.com
letterstoeditores@gmail.com
Abraços,
Pedro.
Não sei o que ocorreu vou procurar saber, por enquanto se desejar pode me mandar um e-mail que eu repasso para os outros adms
Você encontra meu e-mail no meu perfil do blogger
O problema foi resolvido mudamos de e-mail
as figuras não estão carregando pra mim. Não ficou claro para mim como o centróide da figura magicamente apareceu na fórmula desejada. Não entendi a parte final da demonstração.
Postar um comentário