Conjuntos de Cantor generalizados

Uma das construções mais clássicas da matemática é a construção do Conjunto de Cantor. Se você nunca viu um conjunto de Cantor, talvez gostasse de clicar aqui ou aqui. Também fizemos um post sobre o Carpete de Sierpinski, que nada mais é do que uma generalização bidimensional do conjunto de Cantor clássico.

Objetivos e enunciados

Antes de tudo, generalizemos o conceito Conjunto de Cantor na reta.

Definição.  Um conjunto de Cantor generalizado em  é um subconjunto tal que

1. é compacto;
2. é totalmente desconexo;
3. é não-enumerável.

Totalmente desconexo, na reta, significa apenas que o conjunto não contém nenhum intervalo (não-degenerado, i.e., que não se reduz a um único ponto). Cabe observar que esta definição não é padrão, e há muita ambiguidade no termo ``generalizado''.

Qual é o interesse em se construir tais conjuntos? A resposta mais simples é que conjuntos de Cantor fornecem exemplos muito estranhos e contra-intuitivos em Teoria da Medida. Por exemplo, um resultado básico é que todo subconjunto enumerável em  possui medida nula. O conjunto de Cantor clássico produz um contra-exemplo para a recíproca, isto é, é um conjunto não-enumerável mas com medida nula. Vamos nos dedicar neste post a provar o seguinte teorema.

Teorema. Dado , existe um conjunto de Cantor generalizado com medida (de Lebesgue) .

Apenas uma observação: vamos usar a medida de Lebesgue na reta, mas se você não está familiarizado com isto, pode (e deve!) pensar que a medida de um intervalo é simplesmente o seu comprimento; como vamos calcular apenas medidas de intervalos e uniões de intervalos, isto não deve atrapalhar a compreensão do texto.



A construção

Existem muitas formas ad-hoc de obter conjuntos da forma acima, vamos ilustrar aqui um método bastante geral, inspirado na construção do conjunto de Cantor clássico. Por exemplo, veja a construção do livro Counterexamples in Analysis (na sua biblioteca mais próxima!), ou em português neste arquivo pdf. Porém, sempre achei estas exposições um tanto confusas. Espero dar uma abordagem diferente neste post. Para facilitar a comunicação, façamos antes uma definição.

Definição. Seja um intervalo qualquer, com extremos , e . O -meio de é o intervalo aberto

Por exemplo, se , o -meio de é o conjunto , que é um intervalo de tamanho posicionado no meio de . No caso geral, é um intervalo de tamanho posicionado no meio de .

O método é o seguinte: seja uma sequência qualquer com , para todo . Assim como na construção clássica, vamos considerar um processo indutivo, da seguinte maneira: seja , e

1. , onde são intervalos fechados, de mesmo tamanho, e disjuntos entre si;
2. , onde são intervalos fechados, de mesmo tamanho, e disjuntos entre si;
3. ...

É fácil (definir e) mostrar, por indução, que , onde os são intervalos fechados, de mesmo tamanho, e disjuntos entre si. Para visualizar melhor o que está acontecendo, pense no caso em que , para todo , no qual temos o processo indutivo do conjunto de Cantor clássico (veja imagem abaixo). Além disso, temos trivialmente que estes conjuntos estão todos encaixados, i.e., , para todo .

Agora vamos calcular a medida de . Se denota a medida de Lebesgue em , temos 

Agora note que, pela maneira como é construído , temos que . Logo

 

Como , então

Com esta fórmula, provamos rapidamente por indução que

 

Defina, por fim, . Note que, como cada é compacto, então . Além disso, é fácil calcular a medida de :

Observe que este método é bastante geral e poderíamos ter começado com qualquer sequência. Em particular, observe o que acontece se tomamos a sequência : 

Demonstração das propriedades

Resta mostrar agora que , construído a partir de qualquer sequência 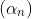, satisfaz as propriedades desejadas. Que é compacto é fácil, pois é claramente limitado e é uma intersecção de conjuntos fechados. Para ver que é totalmente desconexo, suponha um intervalo. Dado qualquer, temos que e, portanto, deve estar contido em algum dos . Em particular, temos que . Como quando , então quando e, portanto, ; o que significa que é um ponto.

Por fim, a parte mais difícil é mostrar que este conjunto é não-enumerável. No conjunto de Cantor clássico, i.e., associado à sequência constante , isto é feito exibindo uma caracterização deste conjunto em termos de uma representação base 3 (a saber, são os pontos em que possuem uma representação terciária que contém apenas os números 0 e 2). Apesar de interessante, este passo é desnecessário. Além do mais, fica difícil saber como generalizamos este argumento para o nosso caso geral. Na verdade, tudo o que precisamos já está aqui: note que, como , dado , temos que, para todo , existe um índice tal que . Assim, podemos associar a a sequência de intervalos ou, de maneira mais simples, a sequência . Note que esta não é uma sequência de naturais qualquer, ela tem a seguinte propriedade: dado , temos que (se ajudar, tente visualizar com um desenho o que está acontecendo). Reciprocamente, se para cada consideramos um intervalo de de tal maneira que , i.e., uma sequência com a propriedade acima, obtemos um único ponto em ! Mais precisamente:

Lema. Existe uma bijeção entre e o conjunto das sequências , com para todo e , .

Demonstração. A cada em , associamos a sequência como acima. Esta aplicação está bem definida (i.e., existe uma única tal sequência) pois os intervalos compondo cada são disjuntos entre si. Esta aplicação é sobrejetora pois, dada uma sequência nas hipóteses acima, então os intervalos fechados estão encaixados e, portanto, e basta tomar pois por definição. Além disso, esta aplicação é injetora. De fato, se e , digamos , estão associados a uma mesma sequência , então para cada e, portanto, . Como já vimos que é totalmente desconexo, se reduz a um ponto, isto é, .

Agora basta mostrar que o conjunto de tais sequências é não-enumerável e, claro :D, vamos usar um argumento do tipo diagonalização de Cantor para isto. Suponha que listamos todas estas sequências:

Seja . Agora, para cada , podemos definir indutivamente $j_n\in \{1,\ldots,2^n\}$ de tal maneira que e (convença-se disso!). Logo é uma sequência bem definida deste conjunto e é diferente de todas as outras sequências listadas acima: e diferem na -ésima coordenada. Absurdo!

Com isto, mostramos tudo o que havíamos proposto neste post. Se você ainda não quer se despedir tão cedo dos conjuntos de Cantor, deixo aqui alguns problemas como diversão.

Problemas

1. Uma outra propriedade usualmente citada quando o conjunto de Cantor é apresentado é que ele é perfeito. Mostre que os conjuntos de Cantor generalizados como acima também são perfeitos (um conjunto é perfeito se ele é igual ao conjunto dos seus pontos de acumulação).
2.  É possível caracterizar as sequências que fornecem conjuntos de Cantor de medida positiva: mostre que se, e somente se, .
3. Você consegue generalizar a construção acima para dimensões maiores, assim como no carpete de Sierpinski?