No post Uma prova topológica para o Teorema de Cayley-Hamilton mostrei como demonstrar o Teorema de Cayley-Hamilton por continuidade, utilizando uma topologia diferente da usual. Porém, esta topologia é tão diferente que algumas boas propriedades, como ser Hausdorff, são perdidas. Este fato fez com que a demonstração ficasse mais complicada (e mais sutil na parte final) do que era para ser.
Neste post, quero apresentar uma outra forma de contornar o problema. Talvez o argumento que irei utilizar seja menos intuitivo, mas com certeza é mais simples, pelo fato de não precisarmos nos preocupar com separabilidade. Se você não leu o primeiro post, clique no link ali em cima.
Neste post, quero apresentar uma outra forma de contornar o problema. Talvez o argumento que irei utilizar seja menos intuitivo, mas com certeza é mais simples, pelo fato de não precisarmos nos preocupar com separabilidade. Se você não leu o primeiro post, clique no link ali em cima.
Teorema. Seja  uma matriz quadrada de ordem
uma matriz quadrada de ordem  , com coeficientes num corpo
, com coeficientes num corpo  , e
, e  seu polinômio característico. Então
seu polinômio característico. Então
Demonstração. Seja  . Como
. Como  é quadrada, de ordem
é quadrada, de ordem  , podemos enxergar
, podemos enxergar  como um elemento de
como um elemento de  . Além disso, o discriminante de
. Além disso, o discriminante de  pode ser visto como um polinômio em
pode ser visto como um polinômio em  variáveis avaliado nos coeficientes de
variáveis avaliado nos coeficientes de  , pois os coeficientes de
, pois os coeficientes de  são polinômios em
são polinômios em 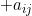 e o discrimininante de
e o discrimininante de  é um polinômio nos coeficientes de
é um polinômio nos coeficientes de  .
.
Assim, podemos falar de um polinômio de variáveis
variáveis  chamado discriminante. Se o discriminante de
chamado discriminante. Se o discriminante de  , ou seja
, ou seja  , é não nulo, então
, é não nulo, então  tem
tem  raízes distintas e
raízes distintas e  é diagonalizável. O conjunto das matrizes cujo discriminante de seu polinômio característico é não nulo, é, portanto,
é diagonalizável. O conjunto das matrizes cujo discriminante de seu polinômio característico é não nulo, é, portanto,  , que é aberto na Topologia de Zariski e, consequentemente, denso em
, que é aberto na Topologia de Zariski e, consequentemente, denso em  .
.
Considere, novamente, o polinômio característico de
de  . Pensando nos coeficientes de
. Pensando nos coeficientes de  como variáveis, então podemos enxergar
como variáveis, então podemos enxergar  como um polinômio de
como um polinômio de  variáveis: os coeficientes
variáveis: os coeficientes 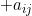 e
e  . Avaliando este polinômio em
. Avaliando este polinômio em  , temos a matriz
, temos a matriz  . Agora, cada uma das
. Agora, cada uma das  entradas de
entradas de  é um polinômio em
é um polinômio em 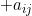 . Sejam
. Sejam  estes polinômios (vou omitir as variáveis para não carregar a notação).
estes polinômios (vou omitir as variáveis para não carregar a notação).
Queremos decidir, então, quais matrizes , i.e., quais elementos de
, i.e., quais elementos de  , satisfazem estes
, satisfazem estes  polinômios. Em outras palavras, queremos saber quais matrizes
polinômios. Em outras palavras, queremos saber quais matrizes  estão no conjunto algébrico
estão no conjunto algébrico  . Mas já sabemos que
. Mas já sabemos que  . Como
. Como  é denso em
é denso em  e
e  é fechado, então
é fechado, então  .
. 
Note que, apesar de não utilizarmos nenhuma função contínua nesta demonstração (em contraponto com a outra), ainda estamos nos aproveitando de um argumento de continuidade, pois dizer que é denso em
é denso em  é dizer que toda matriz
é dizer que toda matriz  está arbitrariamente próxima de uma matriz diagonalizável.
está arbitrariamente próxima de uma matriz diagonalizável.
Utilizando esta mesma ideia deste post, você também pode resolver o desafio do primeiro post de uma maneira mais fácil.
Assim, podemos falar de um polinômio de
Considere, novamente, o polinômio característico
Queremos decidir, então, quais matrizes
Note que, apesar de não utilizarmos nenhuma função contínua nesta demonstração (em contraponto com a outra), ainda estamos nos aproveitando de um argumento de continuidade, pois dizer que
Utilizando esta mesma ideia deste post, você também pode resolver o desafio do primeiro post de uma maneira mais fácil.

3 comentários:
Acho que essa forma é mais simples mesmo =P
Nãaao, o Hamilton chegou atras do Vettel e Alonso pode ser campeão já em interlagos
Pois é, tudo porque ele está sem seu amigo Cayley na equipe.
Postar um comentário